山東省聊城市備考2020年初中數(shù)學(xué)二輪復(fù)習(xí)拔高訓(xùn)練卷 專題11 視圖與投影

《山東省聊城市備考2020年初中數(shù)學(xué)二輪復(fù)習(xí)拔高訓(xùn)練卷 專題11 視圖與投影》由會(huì)員分享，可在線閱讀，更多相關(guān)《山東省聊城市備考2020年初中數(shù)學(xué)二輪復(fù)習(xí)拔高訓(xùn)練卷 專題11 視圖與投影（11頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

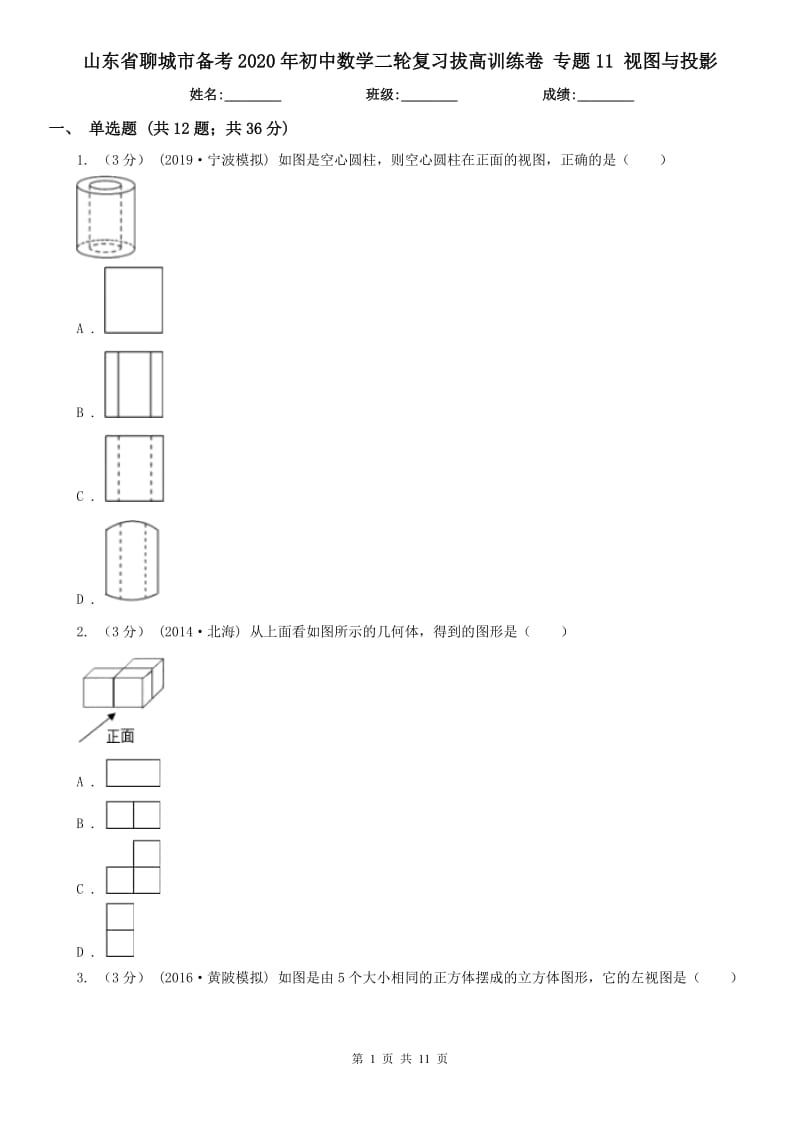
1、山東省聊城市備考2020年初中數(shù)學(xué)二輪復(fù)習(xí)拔高訓(xùn)練卷 專題11 視圖與投影 姓名:________ 班級(jí):________ 成績(jī):________ 一、 單選題 (共12題；共36分) 1. （3分） (2019寧波模擬) 如圖是空心圓柱，則空心圓柱在正面的視圖，正確的是（ ） A . B . C . D . 2. （3分） (2014北海) 從上面看如圖所示的幾何體，得到的圖形是（ ） A . B . C . D . 3. （3分） (2016黃陂模擬) 如圖是由5個(gè)大小相同的正方體

2、擺成的立方體圖形，它的左視圖是（ ） A . B . C . D . 4. （3分） 小明看到了“實(shí)驗(yàn)樓”三個(gè)字，而且能看到該樓所有的門窗，則小明看到的圖是（ ） A . 俯視圖 B . 左視圖 C . 主視圖 D . 都有可能 5. （3分） (2017寧波模擬) 由4個(gè)正方體搭成的幾何體按如圖放置，若要求畫出它的三視圖，則在所畫的俯視圖中正方形共有（ ） A . 1個(gè) B . 2個(gè) C . 3個(gè) D . 4個(gè) 6. （3分） (2012鞍山) 如圖，下面是由四個(gè)完全相同的正方體組成的幾何體，這個(gè)幾何體的主視圖是（ ）

3、 A . B . C . D . 7. （3分） 如圖是由五個(gè)相同的小正方體組成的幾何體，則下列說法正確的是（ ） A . 左視圖面積最大 B . 左視圖面積和主視圖面積相等 C . 俯視圖面積最小 D . 俯視圖面積和主視圖面積相等 8. （3分） 下面四個(gè)幾何體中，左視圖是四邊形的幾何體共有（ ） A . 1個(gè) B . 2個(gè) C . 3個(gè) D . 4個(gè) 9. （3分） (2018九上焦作期末) 如圖所示的四棱柱的主視圖為（ ） A . B . C . D . 11. （3分） (2016龍東)

4、如圖，由5塊完全相同的小正方體所搭成的幾何體的俯視圖，小正方形中的數(shù)字表示在該位置小正方體的個(gè)數(shù)，其主視圖是（ ） A . B . C . D . 12. （3分） 一個(gè)幾何體的三視圖如圖所示，則該幾何體的形狀可能是（ ） A . B . C . D . 二、 填空題 (共8題；共27分) 13. （3分） 如圖是某幾何體的三視圖，根據(jù)圖中數(shù)據(jù)，求得該幾何體的體積為________． ? 14. （3分） (2018白銀) 已知某幾何體的三視圖如圖所示，其中俯視圖為正六邊形，則該幾何體的側(cè)面積為________． 15. （

5、3分） 如圖，由四個(gè)小正方體組成的幾何體中，若每個(gè)小正方體的棱長(zhǎng)都是1，則從上面看到的該幾何體的形狀圖的面積是________． 16. （3分） 如圖所示，平地上一棵樹高為5米，兩次觀察地面上的影子，第一次是當(dāng)陽光與地面成45時(shí)，第二次是陽光與地面成30時(shí)，第二次觀察到的影子比第一次長(zhǎng)________米． 17. （6分） 如圖所示是小紅在某天四個(gè)時(shí)刻看到一個(gè)棒及其影子的情況,那么她看到的先后順序是________． 18. （3分） 下圖右邊是一個(gè)三棱柱，它的正投影是下圖中的________（填序號(hào)）． 19. （3分） 物體在光線的照射下,會(huì)在地面或墻壁上留下它

6、的影子,這就是________現(xiàn)象. 20. （3分） 若干桶方便面擺放在桌子上，如圖是它的三視圖，則這一堆方便面共有________桶． 三、 解答題 (共5題；共37分) 21. （5分） 在Rt△ABC中，∠C=90，AD平分∠CAB，CD=6，AB=10．求△ABD的面積． 22. （6分） (2017七上縣期中) 用小立方塊搭一個(gè)幾何體，主視圖與左視圖如下圖，它最少要多少個(gè)立方塊？最多要多少個(gè)立方塊？畫出這個(gè)幾何體最多、最少兩種情況下的俯視圖，并用數(shù)字表示在該位置的小立方體的個(gè)數(shù)。 23. （6分） (2020九上常州期末) 如圖，在Rt△ABC中，∠C=9

7、0，AC=8，sin A= （1） 求AB的長(zhǎng); （2） 若點(diǎn)E在Rt△ABC的直角邊上，點(diǎn)F在斜邊AB上，當(dāng)△CFE∽△ABC時(shí)，求CE的長(zhǎng). 24. （10分） (2016九上競(jìng)秀期中) 學(xué)習(xí)投影后，小明、小穎利用燈光下自己的影子長(zhǎng)度來測(cè)量一路燈的高度，并探究影子長(zhǎng)度的變化規(guī)律．如圖，在同一時(shí)間，身高為1.6m的小明（AB）的影子BC長(zhǎng)是3m，而小穎（EH）剛好在路燈燈泡的正下方H點(diǎn)，并測(cè)得HB=6m． （1） 請(qǐng)?jiān)趫D中畫出形成影子的光線，并確定路燈燈泡所在的位置G； （2） 求路燈燈泡的垂直高度GH． 25. （10分） 某一廣告墻PQ旁有兩根直立的木

8、桿AB和CD ， 某一時(shí)刻在太陽光下，木桿CD的影子剛好不落在廣告墻PQ上， （1） 你在圖中畫出此時(shí)的太陽光線CE及木桿AB的影子BF； （2） 若AB=5米，CD=3米，CD到PQ的距離DQ的長(zhǎng)為4米，求此時(shí)木桿AB的影長(zhǎng)． 第 11 頁 共 11 頁 參考答案 一、 單選題 (共12題；共36分) 1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 11-1、 12-1、 二、 填空題 (共8題；共27分) 13-1、 14-1、 15-1、 16-1、 17-1、 18-1、 19-1、 20-1、 三、 解答題 (共5題；共37分) 21-1、 22-1、 23-1、 23-2、 24-1、 24-2、 25-1、 25-2、