《高中數(shù)學(xué) 3.1.1方程的根與函數(shù)的零點(diǎn)課件1 新人教A版必修1.ppt》由會(huì)員分享，可在線閱讀，更多相關(guān)《高中數(shù)學(xué) 3.1.1方程的根與函數(shù)的零點(diǎn)課件1 新人教A版必修1.ppt（21頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
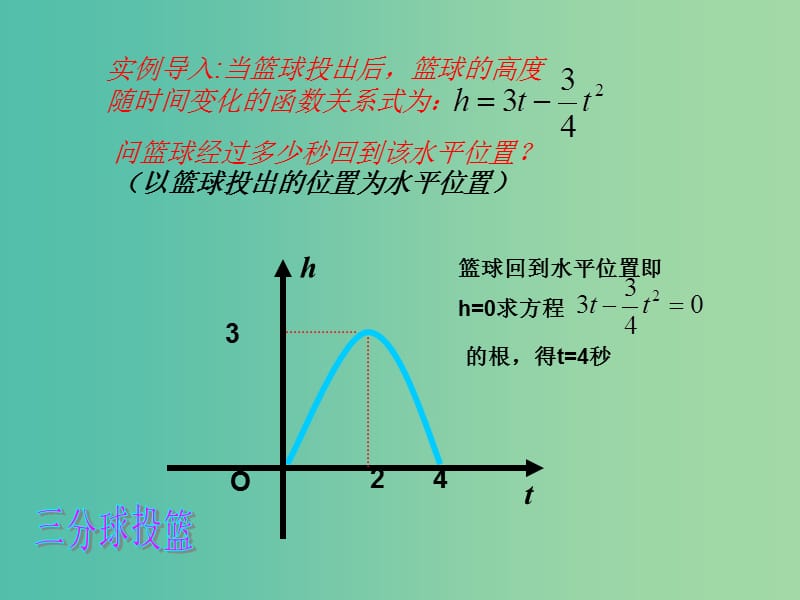
1、實(shí)例導(dǎo)入:當(dāng)籃球投出后，籃球的高度隨時(shí)間變化的函數(shù)關(guān)系式為：,問(wèn)籃球經(jīng)過(guò)多少秒回到該水平位置？（以籃球投出的位置為水平位置）,4,2,3,,,,籃球回到水平位置即 h=0求方程,的根，得t=4秒,三分球投籃,函數(shù)的零點(diǎn)與方程,探究：求下列方程的實(shí)數(shù)根，畫出相應(yīng)函數(shù)的簡(jiǎn)圖， 并求出函數(shù)圖象與x軸交點(diǎn)的坐標(biāo)。,問(wèn)題探究一：,,,-1,3,,,,,,,,,,,-1,,,,1,,,,,,1,2,,,無(wú)實(shí)數(shù)根,,1.方程根的個(gè)數(shù)就是函數(shù)圖象與x軸交點(diǎn)的個(gè)數(shù).,2.方程的實(shí)數(shù)根就是函數(shù)圖象與x軸交點(diǎn)的橫坐標(biāo).,結(jié) 論:,思考：方程根與相應(yīng)函數(shù)圖象有什么聯(lián)系?,對(duì)于函數(shù)y=f(x),我們把使f(x)=0的實(shí)
2、數(shù)x 叫做函數(shù)y=f(x)的零點(diǎn)。,一、函數(shù)零點(diǎn)的定義：,注意：,零點(diǎn)指的是一個(gè)實(shí)數(shù)；,方程f(x)=0有實(shí)數(shù)根,函數(shù)y=f(x)的圖象與x軸有交點(diǎn),函數(shù)y=f(x)有零點(diǎn),,,剖析概念,你能得出什么結(jié)論嗎？,代數(shù)法,圖象法,解析：函數(shù)的零點(diǎn)就是相應(yīng)方程的根.,將函數(shù)f(x)=lnx+2x-6的零點(diǎn)個(gè)數(shù)轉(zhuǎn)化為函數(shù) g(x)=lnx與h(x)=-2x+6的圖象交點(diǎn)的個(gè)數(shù)。,,,想一想： 你能從函數(shù)的性質(zhì)入手分析出它的圖像的大致趨勢(shì)嗎,分析：函數(shù)在定義域（0，+）內(nèi)是增函數(shù)，那么它的函數(shù)值又是怎么變化的？,通過(guò)計(jì)算可知： f(1)=-40,則f(2) f(3)<0，所以它在（2,3）內(nèi)有一個(gè)零點(diǎn),
3、13,,問(wèn)題探究二：怎樣判斷一個(gè)函數(shù)在給定 區(qū)間上是否存在零點(diǎn)呢？,如果函數(shù)y=f(x)在區(qū)間a,b上的圖象是連續(xù) 不斷一條曲線，并且有f(a)f(b)<0，那么， 函數(shù)y=f(x)在區(qū)間(a,b)內(nèi)有零點(diǎn).即存在c(a,b)，使得f(c )=0成立，這個(gè)c也就是方程f(x)=0的根,,連續(xù)函數(shù)在某個(gè)區(qū)間上存在零點(diǎn)的判別方法：,二：定理,思考：若函數(shù)y=f(x)在區(qū)間a,b上連續(xù)，且f(x)在區(qū)間(a,b)內(nèi)有零點(diǎn)，那么一定有f(a)f(b) <0 ?,,,,a,b,0,,,這個(gè)定理反之是不成立的,(c),(2)根據(jù)表格中的數(shù)據(jù)，可以判斷方程exx20的一個(gè)根所在的最小為區(qū)間__________.,解析：設(shè)f(x)exx2，f(1)2.7830.220，f(2)7.3943.390.f(1)f(2)0，由根的存在性定理知，方程exx20必有一個(gè)根在區(qū)間(1,2),
高中數(shù)學(xué) 3.1.1方程的根與函數(shù)的零點(diǎn)課件1 新人教A版必修1.ppt
