2012年中考數(shù)學(xué)復(fù)習(xí)考點(diǎn)跟蹤訓(xùn)練40 探索型問題

《2012年中考數(shù)學(xué)復(fù)習(xí)考點(diǎn)跟蹤訓(xùn)練40 探索型問題》由會(huì)員分享，可在線閱讀，更多相關(guān)《2012年中考數(shù)學(xué)復(fù)習(xí)考點(diǎn)跟蹤訓(xùn)練40 探索型問題（6頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

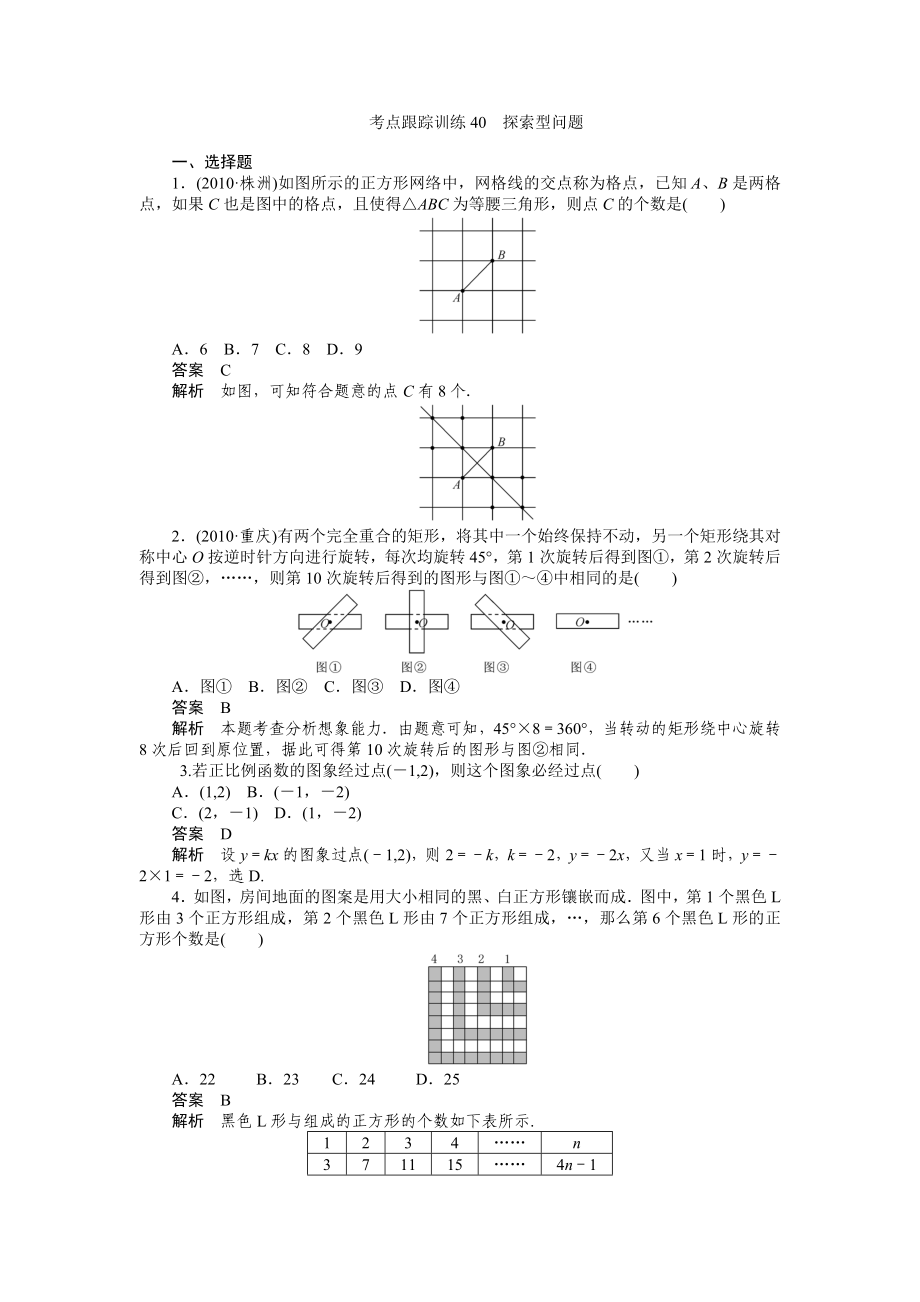
1、考點(diǎn)跟蹤訓(xùn)練40　探索型問題 一、選擇題 1．(2010·株洲)如圖所示的正方形網(wǎng)絡(luò)中，網(wǎng)格線的交點(diǎn)稱為格點(diǎn)，已知A、B是兩格點(diǎn)，如果C也是圖中的格點(diǎn)，且使得△ABC為等腰三角形，則點(diǎn)C的個(gè)數(shù)是(　　) A．6 B．7 C．8 D．9 答案　C 解析　如圖，可知符合題意的點(diǎn)C有8個(gè)． 2．(2010·重慶)有兩個(gè)完全重合的矩形，將其中一個(gè)始終保持不動(dòng)，另一個(gè)矩形繞其對(duì)稱中心O按逆時(shí)針方向進(jìn)行旋轉(zhuǎn)，每次均旋轉(zhuǎn)45°，第1次旋轉(zhuǎn)后得到圖①，第2次旋轉(zhuǎn)后得到圖②，……，則第10次旋轉(zhuǎn)后得到的圖形與圖①～④中相同的是(　　) A．圖① B．圖② C．圖③ D．

2、圖④ 答案　B 解析　本題考查分析想象能力．由題意可知，45°×8＝360°，當(dāng)轉(zhuǎn)動(dòng)的矩形繞中心旋轉(zhuǎn)8次后回到原位置，據(jù)此可得第10次旋轉(zhuǎn)后的圖形與圖②相同． 3.若正比例函數(shù)的圖象經(jīng)過點(diǎn)(－1,2)，則這個(gè)圖象必經(jīng)過點(diǎn)(　　) A．(1,2) B．(－1，－2) C．(2，－1) D．(1，－2) 答案　D 解析　設(shè)y＝kx的圖象過點(diǎn)(－1,2)，則2＝－k，k＝－2，y＝－2x，又當(dāng)x＝1時(shí)，y＝－2×1＝－2，選D. 4．如圖，房間地面的圖案是用大小相同的黑、白正方形鑲嵌而成．圖中，第1個(gè)黑色L形由3個(gè)正方形組成，第2個(gè)黑色L形由7個(gè)正方形組成，…，那么第6個(gè)黑色L

3、形的正方形個(gè)數(shù)是(　　) A．22 B．23 C．24 D．25 答案　B 解析　黑色L形與組成的正方形的個(gè)數(shù)如下表所示. 1 2 3 4 …… n 3 7 11 15 …… 4n－1 當(dāng)n＝6時(shí)，4n－1＝4×6－1＝23.故選B. 5．(2011·潛江)如圖，已知直線l：y＝x，過點(diǎn)A(0,1)作y軸的垂線交直線l于點(diǎn)B，過點(diǎn)B作直線l的垂線交y軸于點(diǎn)A1；過點(diǎn)A1作y軸的垂線交直線l于點(diǎn)B1，過點(diǎn)B1作直線l的垂線交y軸于點(diǎn)A2；…；按此作法繼續(xù)下去，則點(diǎn)A4的坐標(biāo)為(　　) A．(0,64) B．(0,128) C．

4、(0,256) D．(0,512) 答案　C 解析　易求A(0,1)，A1(0,4)，A2(0,16)……，而21＝1,22＝4,24＝16……，所以28＝256，點(diǎn)A4的坐標(biāo)為(0,256)． 二、填空題 6．(2010·鄂爾多斯)如圖，用小棒擺出下面的圖形，圖形(1)需要3根小棒，圖形(2)需要7根小棒，……，照這樣的規(guī)律繼續(xù)擺下去，第n個(gè)圖形需要__________根小棒(用含n的代數(shù)式表示)． 答案　4n－1 解析　圖形(1)有小棒3＝4×1－1；圖形(2)有小棒7＝4×2－1；圖形(3)有小棒11＝4×3－1；……；圖形(n)有小棒4×n－1，即4n－1. 7．(

5、2011·肇慶)如圖所示，把同樣大小的黑色棋子擺放在正多邊形的邊上，按照這樣的規(guī)律擺下去，則第n(n是大于0的整數(shù))個(gè)圖形需要黑色棋子的個(gè)數(shù)是 __________. 答案　n(n＋2) 解析　第1個(gè)圖形需黑色棋子2×3－3個(gè)，第2個(gè)圖形需黑色棋子3×4－4個(gè)，……，則第n個(gè)圖形需黑色棋子個(gè)數(shù)是(n＋1)(n＋2)－(n＋2)＝n2＋2n＝n(n＋2)． 8．(2010·宿遷)如圖，正方形紙片ABCD的邊長(zhǎng)為8，將其沿EF折疊，則圖中①②③④四個(gè)三角形的周長(zhǎng)之和為________． 答案　32 解析　如圖，設(shè)C′B′與AB交點(diǎn)為G′，與AD交點(diǎn)為H′，F(xiàn)C′與AD交點(diǎn)

6、為W′，則這三個(gè)點(diǎn)關(guān)于折痕EF對(duì)稱的點(diǎn)分別為G、H、W，由翻折的性質(zhì)“對(duì)應(yīng)邊相等”，得BE＝EB′，BG＝B′G′，GH＝G′H′，HC＝H′C′，CW＝C′W′，F(xiàn)W＝FW′. ∴①、②、③、④四個(gè)三角形的周長(zhǎng)之和等于正方形的周長(zhǎng)＝4×8＝32. 9．(2011·菏澤)填在下面各正方形中的四個(gè)數(shù)之間都有相同的規(guī)律，根據(jù)這種規(guī)律，m的值是______． 答案　158 解析　根據(jù)左上角0、2、4、6、8、10可知最后一個(gè)正方形是第6個(gè)正方形，陰影部分應(yīng)該是12、14，所以m＝12×14－10＝158. 10．(2011·東莞)如圖(1) ，將一個(gè)正六邊形各邊延長(zhǎng)，構(gòu)成一個(gè)正六角星形

7、AFBDCE，它的面積為1，取△ABC和△DEF各邊中點(diǎn)，連接成正六角星形A1F1B1D1C1E1，如圖(2)中陰影部分；取△A1B1C1和△D1E1F1各邊中點(diǎn)，連接成正六角星形A2F2B2D2C2E2，如圖(3) 中陰影部分；如此下去，則正六角星形AnFnBnDnCnEn的面積為_______． 答案　 解析　正六角星形AFBDCE與正六角形A1F1B1D1C1E1相似，且相似比為2，所以正六角星形A1F1B1D1C1E1的面積是1×2＝，依此類推，正六角星形A2F2B2D2C2E2的面積是×2＝，……，所以正六角星形AnFnBnDnEn的面積是. 三、解答題 11．(2011

8、·成都)設(shè)S1＝1＋＋，S2＝1＋＋，S3＝1＋＋，…， Sn＝1＋＋.設(shè)S＝＋＋…＋，求S的值 (用含n的代數(shù)式表示，其中n為正整數(shù))． 解　Sn＝1＋＋＝1＋2＋2×＝1＋2＋2× ＝2. ∴S＝＋＋＋…＋＝n×1＋ ＝n＋＝n＋＝＝. 12．(2011·雞西)在正方形ABCD的邊AB上任取一點(diǎn)E，作EF⊥AB交BD于點(diǎn)F，取FD的中點(diǎn)G，連接EG、CG，如圖1，易證 EG＝CG且EG⊥CG. (1)將△BEF繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)90°，如圖2，則線段EG和CG有怎樣的數(shù)量關(guān)系和位置關(guān)系？請(qǐng)直接寫出你的猜想； (2)將△BEF繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)180°，如圖3，則線段EG和CG又有

9、怎樣的數(shù)量關(guān)系和位置關(guān)系？請(qǐng)寫出你的猜想，并加以證明． 解　(1)EG＝CG，EG⊥CG. (2)EG＝CG，EG⊥CG. 證明：如圖，延長(zhǎng)FE交DC延長(zhǎng)線于M，連接MG. ∵∠AEM＝90°，∠EBC＝90°，∠BCM＝90°， ∴四邊形BEMC是矩形． ∴BE＝CM，∠EMC＝90°. 又∵BE＝EF， ∴EF＝CM. ∵∠EMC＝90°，F(xiàn)G＝DG， ∴MG＝FD＝FG. ∵BC＝EM ，BC＝CD， ∴EM＝CD. 又∵EF＝CM， ∴FM＝DM. ∴∠F＝45°. 又∵FG＝DG， ∴∠CMG＝∠EMC＝45°. ∴∠F＝∠GMC. ∴△

10、GFE≌△GMC. ∴EG＝CG ，∠FGE＝∠MGC. ∵∠FMC＝90°，MF＝MD，F(xiàn)G＝DG， ∴MG⊥FD， ∴∠FGE＋∠EGM＝90°， ∴∠MGC＋∠EGM＝90°， 即∠EGC＝90°. ∴EG⊥CG. 13．(2011·蘇州)已知二次函數(shù)y＝a(x2－6x＋8)(a>0)的圖象與x軸分別交于點(diǎn)A、B，與y軸交于點(diǎn)C.點(diǎn)D是拋物線的頂點(diǎn)． (1)如圖①，連接AC，將△OAC沿直線AC翻折，若點(diǎn)O的對(duì)應(yīng)點(diǎn)O′恰好落在該拋物線的對(duì)稱軸上，求實(shí)數(shù)a的值； (2)如圖②，在正方形EFGH中，點(diǎn)E、F的坐標(biāo)分別是(4,4)、(4,3)，邊HG位于邊EF的右側(cè)．小林同

11、學(xué)經(jīng)過探索后發(fā)現(xiàn)一個(gè)正確的命題：“若點(diǎn)P是邊EH或邊HG上的任意一點(diǎn)，則四條線段PA、PB、PC、PD不能與任何一個(gè)平行四邊形的四條邊對(duì)應(yīng)相等(即這四條線段不能構(gòu)成平行四邊形)．”若點(diǎn)P是邊EF或邊FG上的任意一點(diǎn)，剛才的結(jié)論是否也成立？請(qǐng)你積極探索，并寫出探索過程； (3)如圖②，當(dāng)點(diǎn)P在拋物線對(duì)稱軸上時(shí)，設(shè)點(diǎn)P的縱坐標(biāo)t是大于3的常數(shù)，試問：是否存在一個(gè)正數(shù)a，使得四條線段PA、PB、PC、PD與一個(gè)平行四邊形的四條邊對(duì)應(yīng)相等(即這四條線段能構(gòu)成平行四邊形)？請(qǐng)說明理由． 解　(1)令y＝0，由a(x2－6x＋8)＝0解得x1＝2，x2＝4； 令x＝0，解得y＝8a. ∴點(diǎn)A、

12、B、C的坐標(biāo)分別是(2,0)、(4,0)、(0,8a)， ∴OA＝2， 該拋物線對(duì)稱軸為直線x＝3. 如圖③，設(shè)拋物線對(duì)稱軸與x軸的交點(diǎn)為M，則AM＝1. 由題意得O′A＝OA＝2， ∴O′A＝2AM，∴∠O′AM＝60°. ∴∠OAC＝∠ O′AC＝60°. ∴OC＝·AO＝2 ，即8a＝2 ，∴a＝. (2)若點(diǎn)P是邊EF或邊FG上的任意一點(diǎn)，結(jié)果同樣成立． (i)如圖④，設(shè)P是邊EF上的任意一點(diǎn)(不與點(diǎn)E重合)，連接PM. ∵點(diǎn)E(4,4)、F(4,3)與點(diǎn)B(4,0)在一直線上，點(diǎn)C在y軸上， ∴PB＜4，PC≥4，∴PC＞PB. 又∵PD＞PM＞PB，

13、PA＞PM＞PB， ∴PB≠PA，PB≠PC，PB≠PD， ∴此時(shí)線段PA、PB、PC、PD不可能構(gòu)成平行四邊形． (ii)設(shè)P是邊FG上的任意一點(diǎn)(不與點(diǎn)G重合)， ∵點(diǎn)F的坐標(biāo)是(4,3)，∴點(diǎn)G的坐標(biāo)是(5,3)． ∴FB＝3，GB＝，∴3≤PB＜. ∵PC≥4，∴PC＞PB. 又∵PD＞PM＞PB，PA＞PM＞PB， ∴PB≠PA，PB≠PC，PB≠PD， ∴此時(shí)線段PA、PB、PC、PD不可能構(gòu)成平行四邊形． (3)存在一個(gè)正數(shù)a，使得四條線段PA、PB、PC、PD與一個(gè)平行四邊形的四條邊對(duì)應(yīng)相等(即這四條線段能夠成平行四邊形)． 如圖⑤，∵點(diǎn)A、B是拋物線與x

14、軸的交點(diǎn)，點(diǎn)P在拋物線對(duì)稱軸上， ∴PA＝PB. ∴當(dāng)PC＝PD時(shí)，線段PA、PB、PC、PD能構(gòu)成平行四邊形． ∵點(diǎn)C的坐標(biāo)是(0,8a)，點(diǎn)D的坐標(biāo)是(3，－a)，點(diǎn)P的坐標(biāo)是(3，t)， ∴PC2＝32＋(t－8a)2，PD2＝(t＋a)2， 由PC＝PD得PC2＝PD2，∴32＋(t－8a)2＝(t＋a)2， 整理得7a2－2ta＋1＝0，∴△＝4t2－28. ∵t是大于3的常數(shù)，∴△＝4t2－28＞0， ∴方程7a2－2ta＋1＝0有兩個(gè)不相等的實(shí)數(shù)根a＝＝， 顯然，a＝＞0，滿足題意． ∴當(dāng)t是一個(gè)大于3的常數(shù)時(shí)，存在一個(gè)正數(shù)a＝，使得線段PA、PB、PC、PD能構(gòu)成平行四邊形．