《人教新課標(biāo)A版 高中數(shù)學(xué)必修3 第二章統(tǒng)計(jì) 2.2樣本估計(jì)總體 2.2.1用樣本的頻率分布估計(jì)總體 同步測試A卷》由會(huì)員分享��,可在線閱讀��,更多相關(guān)《人教新課標(biāo)A版 高中數(shù)學(xué)必修3 第二章統(tǒng)計(jì) 2.2樣本估計(jì)總體 2.2.1用樣本的頻率分布估計(jì)總體 同步測試A卷(15頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�����。
1�、人教新課標(biāo)A版 高中數(shù)學(xué)必修3 第二章統(tǒng)計(jì) 2.2樣本估計(jì)總體 2.2.1用樣本的頻率分布估計(jì)總體 同步測試A卷
姓名:________ 班級(jí):________ 成績:________
一、 單選題 (共15題�����;共30分)
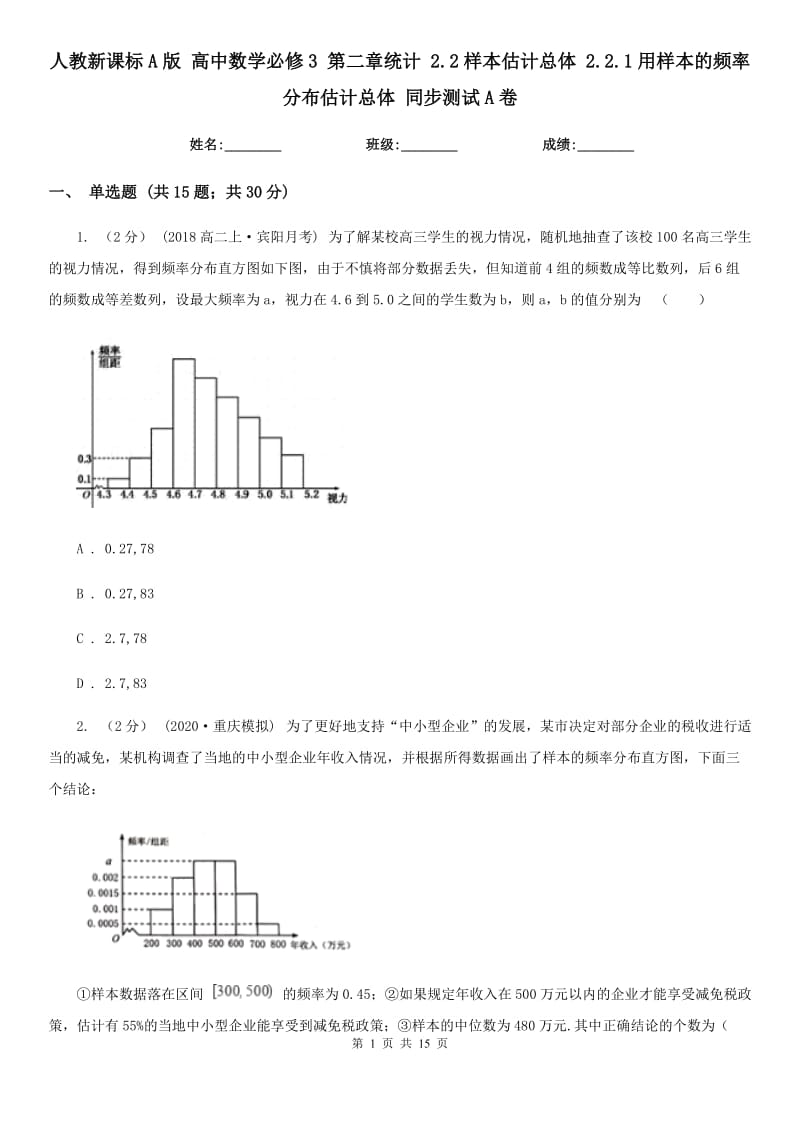
1. (2分) (2018高二上賓陽月考) 為了解某校高三學(xué)生的視力情況�,隨機(jī)地抽查了該校100名高三學(xué)生的視力情況,得到頻率分布直方圖如下圖�����,由于不慎將部分?jǐn)?shù)據(jù)丟失�,但知道前4組的頻數(shù)成等比數(shù)列,后6組的頻數(shù)成等差數(shù)列�,設(shè)最大頻率為a,視力在4.6到5.0之間的學(xué)生數(shù)為b,則a�����,b的值分別為( )
A . 0.
2��、27,78
B . 0.27,83
C . 2.7,78
D . 2.7,83
2. (2分) (2020重慶模擬) 為了更好地支持“中小型企業(yè)”的發(fā)展�,某市決定對(duì)部分企業(yè)的稅收進(jìn)行適當(dāng)?shù)臏p免,某機(jī)構(gòu)調(diào)查了當(dāng)?shù)氐闹行⌒推髽I(yè)年收入情況�����,并根據(jù)所得數(shù)據(jù)畫出了樣本的頻率分布直方圖�,下面三個(gè)結(jié)論:
①樣本數(shù)據(jù)落在區(qū)間 的頻率為0.45�����;②如果規(guī)定年收入在500萬元以內(nèi)的企業(yè)才能享受減免稅政策�,估計(jì)有55%的當(dāng)?shù)刂行⌒推髽I(yè)能享受到減免稅政策;③樣本的中位數(shù)為480萬元.其中正確結(jié)論的個(gè)數(shù)為( )
A . 0
B . 1
C . 2
D . 3
3. (2分) 某校從參加
3�、高二年級(jí)學(xué)業(yè)水平測試的學(xué)生中抽出100名學(xué)生,其數(shù)學(xué)成績的頻率分布直方圖如圖所示.其中成績分組區(qū)間是[40�,50),[50,60)��,[60,70),[70,80)��,[80,90) ,[90,100].則成績在[80 ,100]上的人數(shù)為
A . 70
B . 60
C . 35
D . 30
4. (2分) (2018高二下保山期末) 某校為了提高學(xué)生身體素質(zhì)�,決定組建學(xué)校足球隊(duì),學(xué)校為了解報(bào)名學(xué)生的身體素質(zhì)��,對(duì)他們的體重進(jìn)行了測量�����,將所得的數(shù)據(jù)整理后�����,畫出了頻率分布直方圖(如右圖)�����,已知圖中從左到右3個(gè)小組的頻率之比為1:2:3�,其中第2小組的頻數(shù)為12,則該校報(bào)名學(xué)生總?cè)藬?shù)(
4、 )
A . 40
B . 45
C . 48
D . 50
5. (2分) 統(tǒng)計(jì)某校1000名學(xué)生的數(shù)學(xué)水平測試成績�,得到樣本頻率分布直方圖如圖所示,若滿分為100分��,規(guī)定不低于60分為及格�����,則及格率是( )
A . 20%
B . 25%
C . 6%
D . 80%
6. (2分) 某工廠對(duì)一批產(chǎn)品進(jìn)行了抽樣檢測.右圖是根據(jù)抽樣檢測后的產(chǎn)品凈重(單位:克)數(shù)據(jù)繪制的頻率分布直方圖,其中產(chǎn)品凈重的范圍是[96�����,106]�,樣本數(shù)據(jù)分組為[96,98)�,[98,100)��,[100�,102),[102�,104)�,[104,106]��,已知樣本中產(chǎn)品凈重小于1
5��、00克的個(gè)數(shù)是36�,則樣本中凈重大于或等于98克的產(chǎn)品的個(gè)數(shù)是( )
A . 120
B . 108
C . 90
D . 45
7. (2分) (2016高一下駐馬店期末) 某高校進(jìn)行自主招生,先從報(bào)名者中篩選出400人參加筆試�,再按筆試成績擇優(yōu)選出100人參加面試.現(xiàn)隨機(jī)抽取24名筆試者的成績,如表所示:
分?jǐn)?shù)段
[60,65)
[65�,70)
[70,75)
[75��,80)
[80�,85)
[85,90)
人數(shù)
2
3
4
9
5
1
據(jù)此估計(jì)允許參加面試的分?jǐn)?shù)線大約是( )
A . 90
B . 85
C . 80
D
6�、. 75
8. (2分) 某市高三數(shù)學(xué)抽樣考試中,對(duì)90分以上(含90分)的成績進(jìn)行統(tǒng)計(jì)�,其頻率分布圖如圖所示,已知130~140分?jǐn)?shù)段的人數(shù)為90��,90~100分?jǐn)?shù)段的人數(shù)為a��,則下圖所示程序框圖的運(yùn)算結(jié)果為(注:n?����。?23…n��,如5?����。?2345)( )
A . 800!
B . 810!
C . 811!
D . 812!
9. (2分) (2016高二上孝感期中) 近年來�,隨著私家車數(shù)量的不斷增加��,交通違法現(xiàn)象也越來越嚴(yán)重�,孝感市交警大隊(duì)在某天17:00~20:00這一時(shí)段內(nèi)��,開展整治酒駕專項(xiàng)行動(dòng)��,采取蹲點(diǎn)守候隨機(jī)抽查的方式��,每隔3分鐘檢查一輛經(jīng)過的私家車.
7��、這種抽樣方法屬于( )
A . 簡單隨機(jī)抽樣
B . 系統(tǒng)抽樣
C . 分層抽樣
D . 定點(diǎn)抽樣
10. (2分) 已知樣本7�����,10�,14,8��,7�,12�,11,10�����,8,10�����,13�����,10�����,8��,11�,8,9��,12�����,9��,13�����,20,那么這組數(shù)據(jù)落在8.5~11.5的頻率為( )
A . 0.5
B . 0.4
C . 0.3
D . 0.2
11. (2分) (2020阜陽模擬) 某單位去年的開支分布的折線圖如圖1所示��,在這一年中的水�、電、交通開支(單位:萬元)如圖2所示�,則該單位去年的水費(fèi)開支占總開支的百分比為( )
A .
B .
C
8、.
D .
12. (2分) 從一堆蘋果中任取20粒��,稱得各粒蘋果的質(zhì)量(單位:克)數(shù)據(jù)分布如下表所示:
分組
[100�,110]
(110,120]
(120��,130]
(130�,140]
(140,150]
(150��,160]
頻數(shù)
1
3
4
6
a
2
根據(jù)頻數(shù)分布表�����,可以估計(jì)在這堆蘋果中��,質(zhì)量大于130克的蘋果數(shù)約占蘋果總數(shù)的( )
A . 10%
B . 30%
C . 60%
D . 80%
13. (2分) 為了了解某地參加計(jì)算機(jī)水平測試的5000名學(xué)生的成績�����,從中抽取了200名學(xué)生的成績進(jìn)行統(tǒng)計(jì)分析.在這個(gè)問題中�,5000
9、名學(xué)生成績的全體是( )
A . 總體
B . 個(gè)體
C . 從總體中抽取的一個(gè)樣本
D . 樣本的容量
14. (2分) 在投擲一枚硬幣的試驗(yàn)中�����,共投擲了100次�����,“正面朝上”的頻數(shù)49�,則“正面朝上”的頻率為( )
A . 0.49
B . 0.5
C . 0.51
D . 49
15. (2分) 下列說法正確的是( )
A . 根據(jù)樣本估計(jì)總體,其誤差與所選擇的樣本容量無關(guān)
B . 方差和標(biāo)準(zhǔn)差具有相同的單位
C . 從總體中可以抽取不同的幾個(gè)樣本
D . 如果容量相同的兩個(gè)樣本的方差滿足S12<S22 �����, 那么推得總體也滿足S12<S22
10�、
二、 填空題 (共5題��;共5分)
16. (1分) 某網(wǎng)絡(luò)公司為了調(diào)查一住宅區(qū)連接互聯(lián)網(wǎng)情況�,從該住宅區(qū)28000住戶中隨機(jī)抽取了210戶進(jìn)行調(diào)查,調(diào)查數(shù)據(jù)如右圖�,則估計(jì)該住宅區(qū)已接入互聯(lián)網(wǎng)的住戶數(shù)是________.
17. (1分) 某中學(xué)舉行了一次田徑運(yùn)動(dòng)會(huì)��,其中有50名學(xué)生參加了一次百米比賽�����,他們的成績和頻率如圖所示.若將成績小于15秒作為獎(jiǎng)勵(lì)的條件,則在這次百米比賽中獲獎(jiǎng)的人數(shù)共有________人.
18. (1分) (2017茂名模擬) 如圖為某工廠工人生產(chǎn)能力頻率分布直方圖��,則估計(jì)此工廠工人生產(chǎn)能力的平均值為________
19. (1分) (201
11�����、6高一下中山期中) 超速行駛已成為馬路上最大殺手之一��,已知某中段屬于限速路段�,規(guī)定通過該路段的汽車時(shí)速不超過80km/h,否則視為違規(guī).某天�����,有1000輛汽車經(jīng)過了該路段�����,經(jīng)過雷達(dá)測速得到這些汽車運(yùn)行時(shí)速的頻率分布直方圖如圖所示,則違規(guī)的汽車大約為________輛.
20. (1分) 對(duì)某文科班50名同學(xué)的一次數(shù)學(xué)成績進(jìn)行了統(tǒng)計(jì)�,全年級(jí)文科數(shù)學(xué)平均分是100分�,這個(gè)班數(shù)學(xué)成績的頻率分布直方圖如圖:(總分150分)從這個(gè)班中任取1人�,其數(shù)學(xué)成績達(dá)到或超過年級(jí)文科平均分的概率是________.
三��、 解答題 (共5題�;共25分)
21. (5分) 某中學(xué)對(duì)高三年級(jí)進(jìn)行身高統(tǒng)計(jì)
12��、�����,測量隨機(jī)抽取的40名學(xué)生的身高,其結(jié)果如下(單位:cm)
分組
[140��,145)
[145�,150)
[150,155)
[155�����,160)
[160,165)
[165��,170)
[170�,175)
[175,180)
合計(jì)
人數(shù)
1
2
5
9
13
6
3
1
40
(1) 列出頻率分布表�����;
(2) 畫出頻率分布直方圖�;
(3) 估計(jì)數(shù)據(jù)落在[150,170]范圍內(nèi)的概率.
22. (5分) (2018高二上宜昌期末) 某班50名學(xué)生在一次數(shù)學(xué)測試中�,成績?nèi)拷橛?0與100之間,將測試結(jié)果按如下方式分成五組:第一組[50�,60
13、)��,第二組[60��,70)�,…��,第五組[90�����,100].如圖所示是按上述分組方法得到的頻率分布直方圖.
(Ⅰ)若成績大于或等于60且小于80,認(rèn)為合格�,求該班在這次數(shù)學(xué)測試中成績合格的人數(shù);
(Ⅱ)從測試成績在[50�����,60)∪[90�,100]內(nèi)的所有學(xué)生中隨機(jī)抽取兩名同學(xué)��,設(shè)其測試成績分別為m�、n,求事件“|m﹣n|>10”概率.
23. (5分) 空氣質(zhì)量指數(shù)PM2.5(單位:μg/m3)表示每立方米空氣中可入肺顆粒物的含量�,這個(gè)值越高,解代表空氣污染越嚴(yán)重:
PM2.5日均濃度
0~35
35~75
75~115
115~150
150~250
>250
空氣質(zhì)量級(jí)
14�、別
一級(jí)
二級(jí)
三級(jí)
四級(jí)
五級(jí)
六級(jí)
空氣質(zhì)量類別
優(yōu)
良
輕度污染
中度污染
重度污染
嚴(yán)重污染
某市2012年3月8日﹣4月7日(30天)對(duì)空氣質(zhì)量指數(shù)PM2.5進(jìn)行檢測,獲得數(shù)據(jù)后整理得到如圖條形圖:
(1)估計(jì)該城市一個(gè)月內(nèi)空氣質(zhì)量類別為良的概率�;
(2)從空氣質(zhì)量級(jí)別為三級(jí)和四級(jí)的數(shù)據(jù)中任取2個(gè),求至少有一天空氣質(zhì)量類別為中度污染的概率.
24. (5分) 寫出下列各題的抽樣過程
(1)請從擁有500個(gè)分?jǐn)?shù)的總體中用簡單隨機(jī)抽樣方法抽取一個(gè)容量為30的樣本.
(2)某車間有189名職工�,現(xiàn)在要按1:21的比例選派質(zhì)量檢查員,采用系統(tǒng)抽樣的方
15�����、式進(jìn)行.
(3)一個(gè)電視臺(tái)在因特網(wǎng)上就觀眾對(duì)某一節(jié)目喜愛的測得進(jìn)行得出��,車間得出的總?cè)藬?shù)為12000人,其中持各種態(tài)度的人數(shù)如下:
很喜愛喜愛一般不喜愛
2435456739261072
打算從中抽取60人進(jìn)行詳細(xì)調(diào)查�,如何抽取�?
25. (5分) (2020漳州模擬) 某市場研究人員為了了解產(chǎn)業(yè)園引進(jìn)的甲公司前期的經(jīng)營狀況,對(duì)該公司2018年連續(xù)六個(gè)月的利潤進(jìn)行了統(tǒng)計(jì)��,并根據(jù)得到的數(shù)據(jù)繪制了相應(yīng)的折線圖�����,如圖所示
參考數(shù)據(jù):
參考公式:回歸直線方程 ��,其中
(1) 由折線圖可以看出�����,可用線性回歸模型擬合月利潤 (單位:百萬元)與月份代碼 之間的關(guān)系�����,求 關(guān)
16�����、于 的線性回歸方程��,并預(yù)測該公司2019年3月份的利潤;
(2) 甲公司新研制了一款產(chǎn)品�,需要采購一批新型材料,現(xiàn)有 兩種型號(hào)的新型材料可供選擇�,按規(guī)定每種新型材料最多可使用 個(gè)月,但新材料的不穩(wěn)定性會(huì)導(dǎo)致材料損壞的年限不同�,現(xiàn)對(duì) 兩種型號(hào)的新型材料對(duì)應(yīng)的產(chǎn)品各 件進(jìn)行科學(xué)模擬測試,得到兩種新型材料使用壽命的頻數(shù)統(tǒng)計(jì)如下表:
使用壽命/材料類型
1個(gè)月
2個(gè)月
3個(gè)月
4個(gè)月
總計(jì)
A
20
35
35
10
100
B
10
30
40
20
100
如果你是甲公司的負(fù)責(zé)人�����,你會(huì)選擇采購哪款新型材料�����?
第 15 頁 共 15 頁
參考答案
一�、 單選題 (共15題�����;共30分)
1-1��、
2-1�、
3-1、
4-1�����、
5-1、
6-1�����、
7-1��、
8-1�、
9-1、
10-1�、
11-1、
12-1�、
13-1、
14-1�����、
15-1�����、
二�、 填空題 (共5題;共5分)
16-1�����、
17-1、
18-1�����、
19-1��、
20-1��、
三��、 解答題 (共5題�����;共25分)
21-1�、
21-2�����、
21-3�、
22-1、
23-1��、
24-1、
25-1�����、
25-2��、
 人教新課標(biāo)A版 高中數(shù)學(xué)必修3 第二章統(tǒng)計(jì) 2.2樣本估計(jì)總體 2.2.1用樣本的頻率分布估計(jì)總體 同步測試A卷
人教新課標(biāo)A版 高中數(shù)學(xué)必修3 第二章統(tǒng)計(jì) 2.2樣本估計(jì)總體 2.2.1用樣本的頻率分布估計(jì)總體 同步測試A卷