《2021八年級數(shù)學(xué)下冊 第1章 第3節(jié) 直角三角形全等的判定教案 (新版)湘教版》由會(huì)員分享�,可在線閱讀,更多相關(guān)《2021八年級數(shù)學(xué)下冊 第1章 第3節(jié) 直角三角形全等的判定教案 (新版)湘教版(2頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
1、
直角三角形全等的判定
課題
直角三角形全等的判定
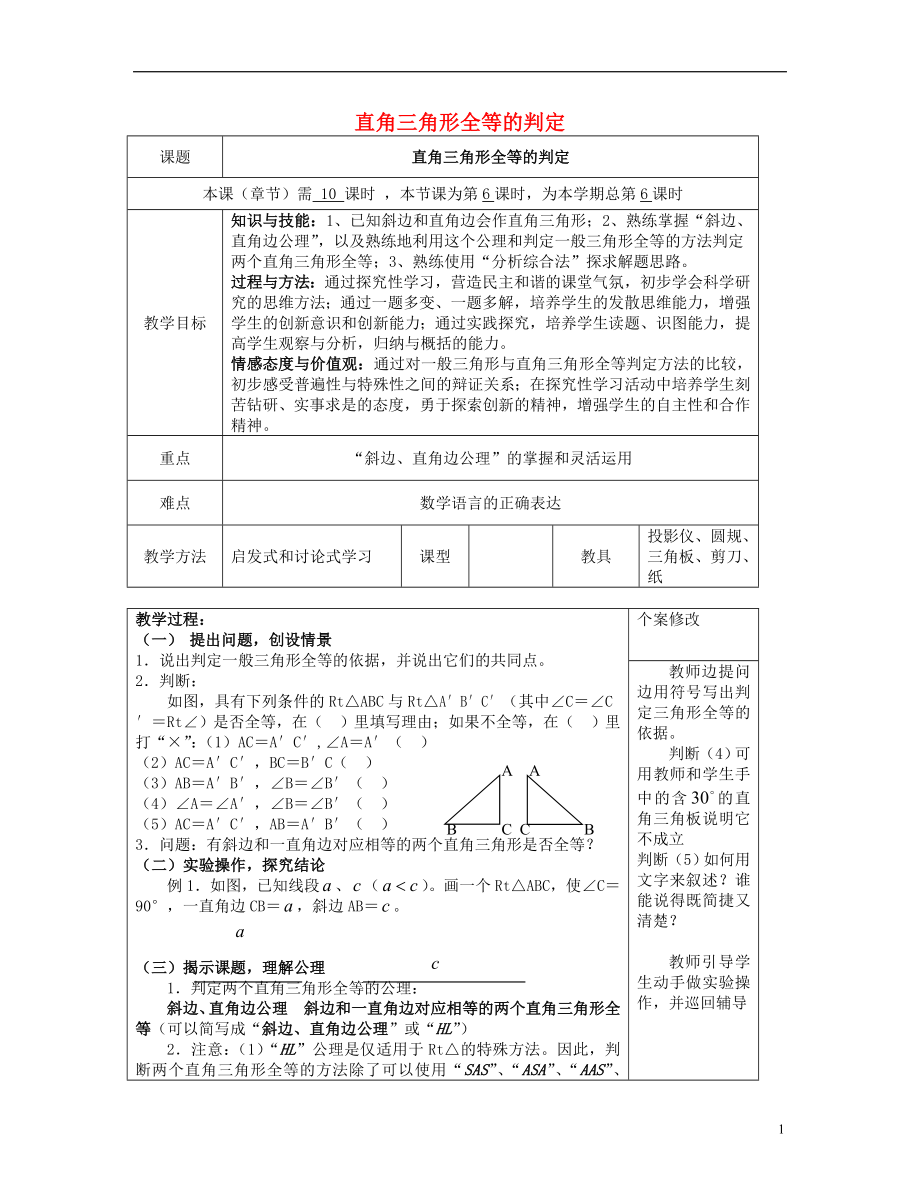
本課(章節(jié))需 10 課時(shí) �,本節(jié)課為第6課時(shí),為本學(xué)期總第6課時(shí)
教學(xué)目標(biāo)
知識與技能:1�、已知斜邊和直角邊會(huì)作直角三角形;2�、熟練掌握“斜邊、直角邊公理”�,以及熟練地利用這個(gè)公理和判定一般三角形全等的方法判定兩個(gè)直角三角形全等�;3、熟練使用“分析綜合法”探求解題思路�。
過程與方法:通過探究性學(xué)習(xí),營造民主和諧的課堂氣氛�,初步學(xué)會(huì)科學(xué)研究的思維方法;通過一題多變�、一題多解,培養(yǎng)學(xué)生的發(fā)散思維能力,增強(qiáng)學(xué)生的創(chuàng)新意識和創(chuàng)新能力�;通過實(shí)踐探究,培養(yǎng)學(xué)生讀題�、識圖能力,提高學(xué)生觀察與分析�,歸納與概括的能力。
情感態(tài)度與價(jià)值觀:通過
2�、對一般三角形與直角三角形全等判定方法的比較,初步感受普遍性與特殊性之間的辯證關(guān)系�;在探究性學(xué)習(xí)活動(dòng)中培養(yǎng)學(xué)生刻苦鉆研、實(shí)事求是的態(tài)度�,勇于探索創(chuàng)新的精神,增強(qiáng)學(xué)生的自主性和合作精神�。
重點(diǎn)
“斜邊、直角邊公理”的掌握和靈活運(yùn)用
難點(diǎn)
數(shù)學(xué)語言的正確表達(dá)
教學(xué)方法
啟發(fā)式和討論式學(xué)習(xí)
課型
教具
投影儀�、圓規(guī)、三角板�、剪刀、紙
教學(xué)過程:
(一) 提出問題�,創(chuàng)設(shè)情景
1.說出判定一般三角形全等的依據(jù),并說出它們的共同點(diǎn)�。
2.判斷:
B′
A
A′
B
C
C′
如圖,具有下列條件的Rt△ABC與Rt△A′B′C′(其中∠C=∠C′=Rt∠)是否全
3�、等,在(?。├锾顚懤碛桑蝗绻蝗龋冢ā�。├锎颉啊痢保海?)AC=A′C′,∠A=A′( )
(2)AC=A′C′�,BC=B′C( )
(3)AB=A′B′�,∠B=∠B′( )
(4)∠A=∠A′�,∠B=∠B′( )
(5)AC=A′C′�,AB=A′B′( )
3. 問題:有斜邊和一直角邊對應(yīng)相等的兩個(gè)直角三角形是否全等�?
(二)實(shí)驗(yàn)操作,探究結(jié)論
例1.如圖�,已知線段、()�。畫一個(gè)Rt△ABC,使∠C=90°�,一直角邊CB=,斜邊AB=�。
(三)揭示課題,理解公理
1.判定兩個(gè)直角三角形全等的公理:
斜邊�、直角邊公理 斜邊和一直角邊對應(yīng)相等的兩個(gè)直角三角
4�、形全等(可以簡寫成“斜邊、直角邊公理”或“HL”)
2.注意:(1)“HL”公理是僅適用于Rt△的特殊方法�。因此,判斷兩個(gè)直角三角形全等的方法除了可以使用“SAS”、“ASA”�、“AAS”、“SSS”外�,還可以使用“HL”。(2)應(yīng)用HL公理時(shí)�,雖只有兩個(gè)條件,但必須先有兩個(gè)Rt△�。書寫格式為:
在Rt△______和Rt△______中,
∴Rt△______≌Rt△______(HL)
(四)鞏固練習(xí)�,達(dá)成目標(biāo)
1.已知:如圖,△ABC中�,AB=AC,AD是高�,則______≌______。依據(jù)是______,BD=______,∠BAD=______.
A
B
C
5�、D
E
C
A
D
B
B′
D′
C′
A′
A
B
D
C
A
B
C
D
2.如圖,已知∠ACB=∠BDA=90°�,若要使△ACB≌△BDA,還需要什么條件�?把它們分別寫出來。
(五)發(fā)散探究�,強(qiáng)化目標(biāo)
例:已知如上圖,在△ABC和△A′B′C′中�,CD、C′D′分別是高�,并且AC=A′C′�,CD=C′D′�,∠ACB=∠A′C′B′。求證:△ABC≌△A′B′C′
變式1:若例題中的∠ACB=∠A′C′B′改為AB=A′B′�,△ABC與△A′B′C′全等嗎?請說明思路�。
變式2:若例題中的∠ACB=∠A′C′B′改為
6、BC=B′C′�,△ABC與△A′B′C′全等嗎?請說明思路�。
變式3::請你把例題中的∠ACB=∠A′C′B′改為另一個(gè)適當(dāng)條件,使△ABC與△A′B′C′仍能全等�。試說明證明思路。
(六)歸納總結(jié)�,深化目標(biāo)
1.直角三角形全等的判定方法有四項(xiàng)依據(jù):“SAS”、“ASA”�、“AAS”、“SSS”“HL”其中�,“HL”公理只適用判定直角三角形全等。2.使用“HL”公理時(shí)�,必須先得出兩個(gè)直角三角形,然后證明斜邊和一直角邊對應(yīng)相等�。3.熟練使用“分析綜合法”探求解題思路。
(七)檢測反饋�,回授目標(biāo)
1.“HL”公理是:有__相等的兩個(gè)_三角形全等。
2.在應(yīng)用“HL”公理時(shí)�,必須先得
7、出兩個(gè)_三角形�,然后證明_______對應(yīng)相等。
3. 如圖�,AB=AC,CD⊥AB于D�,BE⊥AC于E,則圖中全等的三角形對數(shù)為(?。?
(A)1 (B)2 ?。–)3 (D)4
并求證:Rt?BEC≌Rt?CDB.
證明過程見教材P20例1�。
4、自學(xué)教材P20 例2
作業(yè):
教材:P21第1 ~6題
個(gè)案修改
教師邊提問邊用符號寫出判定三角形全等的依據(jù)�。
判斷(4)可用教師和學(xué)生手中的含的直角三角板說明它不成立
判斷(5)如何用文字來敘述?誰能說得既簡捷又清楚�?
教師引導(dǎo)學(xué)生動(dòng)手做實(shí)驗(yàn)操作,并巡回輔導(dǎo)
教師講解:“HL”的由來�。
啟發(fā)提問:在使用這個(gè)公理時(shí)同學(xué)們應(yīng)注意什么?
教師出示投影�,啟發(fā)學(xué)生歸納證明兩個(gè)直角三角形全等的方法,掌握正確使用公理進(jìn)行推理的方法�。
巡視指導(dǎo),師生互動(dòng)�,啟發(fā)學(xué)生分析探索充分條件。
提問板演�,及時(shí)評價(jià)激勵(lì)�,及時(shí)彌補(bǔ)
2
 2021八年級數(shù)學(xué)下冊 第1章 第3節(jié) 直角三角形全等的判定教案 (新版)湘教版
2021八年級數(shù)學(xué)下冊 第1章 第3節(jié) 直角三角形全等的判定教案 (新版)湘教版