2022年高考數學二輪復習 專題五 立體幾何 專題突破練15 空間中的平行與幾何體的體積 文

《2022年高考數學二輪復習 專題五 立體幾何 專題突破練15 空間中的平行與幾何體的體積 文》由會員分享，可在線閱讀，更多相關《2022年高考數學二輪復習 專題五 立體幾何 專題突破練15 空間中的平行與幾何體的體積 文（7頁珍藏版）》請在裝配圖網上搜索。

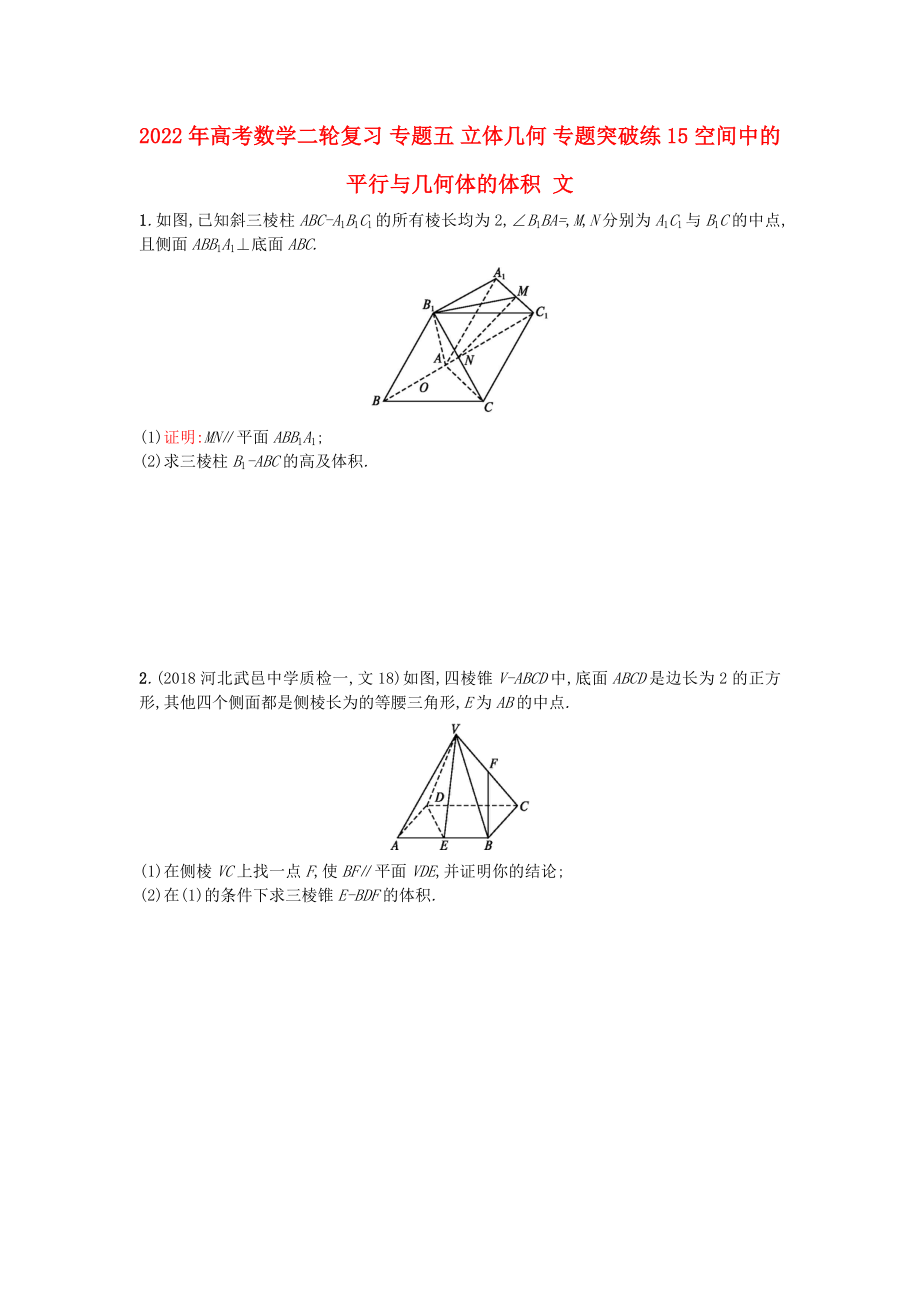
1、2022年高考數學二輪復習 專題五 立體幾何 專題突破練15 空間中的平行與幾何體的體積 文 1.如圖,已知斜三棱柱ABC-A1B1C1的所有棱長均為2,∠B1BA=,M,N分別為A1C1與B1C的中點,且側面ABB1A1⊥底面ABC. (1)證明:MN∥平面ABB1A1; (2)求三棱柱B1-ABC的高及體積. 2.(2018河北武邑中學質檢一,文18)如圖,四棱錐V-ABCD中,底面ABCD是邊長為2的正方形,其他四個側面都是側棱長為的等腰三角形,E為AB的中點. (1)在側棱VC上找一點F,使BF∥平面VDE,并證明你的結論; (2)在

2、(1)的條件下求三棱錐E-BDF的體積. 3. 如圖,在四棱錐P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB與△PAD都是邊長為2的等邊三角形,E是BC的中點. (1)求證:AE∥平面PCD; (2)求四棱錐P-ABCD的體積. 4.(2018遼寧撫順一模,文18)如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,底面ABCD為梯形,AB∥CD,∠BAD=60°,PD=AD=AB=2,CD=4,E為PC的中點. (1)證明:BE∥平面PAD;

3、 (2)求三棱錐E-PBD的體積. 5.(2018全國卷2,文19)如圖,在三棱錐P-ABC中,AB=BC=2,PA=PB=PC=AC=4,O為AC的中點. (1)證明:PO⊥平面ABC; (2)若點M在棱BC上,且MC=2MB,求點C到平面POM的距離. 6.如圖,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,點M是棱CC1的中點. (1)在棱AB上是否存在一點N,使MN∥平面AB1C1?若存在,請確定點N的位置.若不存在,請說明理由; (2)當△ABC是等邊三角形,

4、且AC=CC1=2時,求點M到平面AB1C1的距離. 7.如圖,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,∠BCC1=,AB=BB1=2,BC=1,D為CC1的中點. (1)求證:DB1⊥平面ABD; (2)求點A1到平面ADB1的距離. 8.(2018百校聯盟四月聯考,文19)如圖,在幾何體ABCDEF中,底面CDEF是平行四邊形,AB∥CD,AB=1,CD=2,DE=2,DF=4,DB=2,DB⊥平面CDEF,CE與DF交于點O. (1)求證:OB∥平面A

5、CF; (2)求三棱錐B-DEF的表面積. 參考答案 專題突破練15　空間中的平行與 幾何體的體積 1.(1)證明 取AC的中點P,連接PN,PM. ∵在斜三棱柱ABC-A1B1C1中,M,N分別為A1C1與B1C的中點, ∴PN∥AB1,PM∥AA1. ∵PM∩PN=P,AB1∩AA1=A,PM,PN?平面PMN,AB1,AA1?平面AB1A1,∴平面PMN∥平面AB1A1. ∵MN?平面PMN, ∴MN∥平面ABB1A1. (2)解 設O為AB的中點,連接B1O,由題意知△B1BA

6、是正三角形,則B1O⊥AB. ∵側面ABB1A1⊥底面ABC,且交線為AB,∴B1O⊥平面ABC,∴三棱柱B1-ABC的高B1O=AB1=. ∵S△ABC=×2×2×sin 60°=, ∴三棱柱B1-ABC的體積V=S△ABC·B1O==1. 2.解 (1)F為VC的中點.取CD的中點H,連接BH,HF, ∵ABCD為正方形,E為AB的中點, ∴BE􀱀DH,∴BH∥DE. ∵FH∥VD,∴平面BHF∥平面VDE. ∴BF∥平面VDE. (2)∵F為VC的中點,S△BDE=S正方形ABCD, ∴VE-BDF=VF-BDE=VV-ABCD. ∵V-ABC

7、D為正四棱錐,∴V在平面ABCD內的射影為AC的中點O, ∵VA=,AO=,∴VO=. ∴VV-ABCD=×22×, ∴VE-BDF=. 3.(1)證明 ∵∠ABC=∠BAD=90°, ∴AD∥BC. ∵BC=2AD,E是BC的中點, ∴AD=CE, ∴四邊形ADCE是平行四邊形, ∴AE∥CD. 又AE?平面PCD,CD?平面PCD, ∴AE∥平面PCD. (2)解 連接DE,BD,設AE∩BD=O,連接OP, 則四邊形ABED是正方形, ∴O為BD的中點. ∵△PAB與△PAD都是邊長為2的等邊三角形, ∴BD=2,OB=,OA=,PA=PB=2,∴OP

8、⊥OB,OP=,∴OP2+OA2=PA2,即OP⊥OA.又OA?平面ABCD,BD?平面ABCD,OA∩OB=O, ∴OP⊥平面ABCD. ∴VP-ABCD=S梯形ABCD·OP=×(2+4)×2×=2. 4.(1)證明 設F為PD的中點,連接EF,FA. 因為EF為△PDC的中位線, 所以EF∥CD,且EF=CD=2. 又AB∥CD,AB=2,所以AB􀱀EF, 故四邊形ABEF為平行四邊形,所以BE∥AF.又AF?平面PAD,BE?平面PAD,所以BE∥平面PAD. (2)解 因為E為PC的中點,所以三棱錐VE-PBD=VE-BCD=VP-BCD. 又

9、AD=AB,∠BAD=60°,所以△ABD為等邊三角形.因此BD=AB=2. 又CD=4,∠BDC=∠BAD=60°,所以BD⊥BC,因為PD⊥平面ABCD, 所以三棱錐P-BCD的體積VP-BCD=PD·S△BCD=×2××2×2.所以三棱錐E-PBD的體積VE-PBD=. 5. 解 (1)因為AP=CP=AC=4,O為AC的中點,所以OP⊥AC,且OP=2. 連接OB,因為AB=BC=AC,所以△ABC為等腰直角三角形,且OB⊥AC,OB=AC=2. 由OP2+OB2=PB2知,OP⊥OB. 由OP⊥OB,OP⊥AC知PO⊥平面ABC. (2)作CH⊥OM,垂足為H.又

10、由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的長為點C到平面POM的距離. 由題設可知OC=AC=2,CM=BC=,∠ACB=45°.所以OM=,CH=. 所以點C到平面POM的距離為. 6.解 (1)在棱AB上存在中點N,使MN∥平面AB1C1,證明如下: 設BB1的中點為D,連接DM,NM,ND,因為點M,N,D是CC1,AB,BB1的中點, 所以ND∥AB1,DM∥B1C1,所以ND∥平面AB1C1,DM∥平面AB1C1. 又ND∩DM=D,所以平面NDM∥平面AB1C1.因為MN?平面NDM,所以MN∥平面AB1C1. (2)因為MN∥平面AB1C1,所以點M

11、到平面AB1C1的距離與點N到平面AB1C1的距離相等. 又點N為AB的中點,所以點N到平面AB1C1的距離等于點B到平面AB1C1的距離的一半. 因為AA1⊥平面ABC,所以AB1=AC1=2,所以△AB1C1的底邊B1C1上的高為. 設點B到平面AB1C1的距離為h,則由,得×2××2××h,可得h=,故點M到平面AB1C1的距離為. 7.(1)證明 在四邊形BCC1B1中, ∵BC=CD=DC1=1,∠BCD=, ∴BD=1. ∵B1D=,BB1=2,∴B1D⊥BD. ∵AB⊥平面BCC1B1,∴AB⊥DB1, ∴DB1⊥平面ABD. (2)解 對于四面體A1ADB1

12、,A1到直線DB1的距離即為A1到平面BB1C1C的距離,A1到DB1的距離為2.設A1到平面ADB1的距離為h,△ADB1為直角三角形,AD·DB1=,∴×h=h.∵×2×2=2,D到平面AA1B1的距離為, ∴×2×. ∵,∴,解得h=. ∴點A1到平面ADB1的距離為. 8.(1)證明 取CF中點G,連接AG,OG, 在△CDF中,O是DF的中點,G是CF的中點, ∴OG∥CD,OG=CD, 又AB∥CD,AB=1,CD=2, ∴OG∥AB,OG=AB, ∴四邊形ABOG為平行四邊形, ∴OB∥AG,∵AG?平面ACF,OB?平面ACF,故OB∥平面ACF. (

13、2)解 由EF=CD=2,DE=2,DF=4, 可得EF2+DF2=DE2,所以EF⊥DF.∴△DEF的面積S1=×DF×EF=×4×2=4. 由DB⊥平面CDEF,DF?平面CDEF,DE?平面CDEF,EF?平面CDEF,可得BD⊥DF,BD⊥DE,BD⊥EF,∴△BDF的面積S2=×BD×DF=×2×4=4,△BDE的面積S3=×BD×DE=×2×2=2, 由EF⊥DF,EF⊥BD,BD∩DF=D, 可得EF⊥平面BDF. 又BF?平面BDF,所以EF⊥BF. ∵BF==2, ∴△BEF的面積S4=×BF×EF=×2×2=2, ∴三棱錐B-DEF的表面積S=S1+S2+S3+S4=8+4.