2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1

上傳人：xt****7 文檔編號：105234887 上傳時間：2022-06-11 格式：DOC 頁數(shù)：2 大?。?90.02KB
收藏 版權申訴 舉報 下載
2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1_第1頁
第1頁 / 共2頁
2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1_第2頁
第2頁 / 共2頁

最后一頁預覽完了！喜歡就下載吧，查找使用更方便

9.9 積分

下載資源

資源描述：

《2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1》由會員分享，可在線閱讀，更多相關《2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。

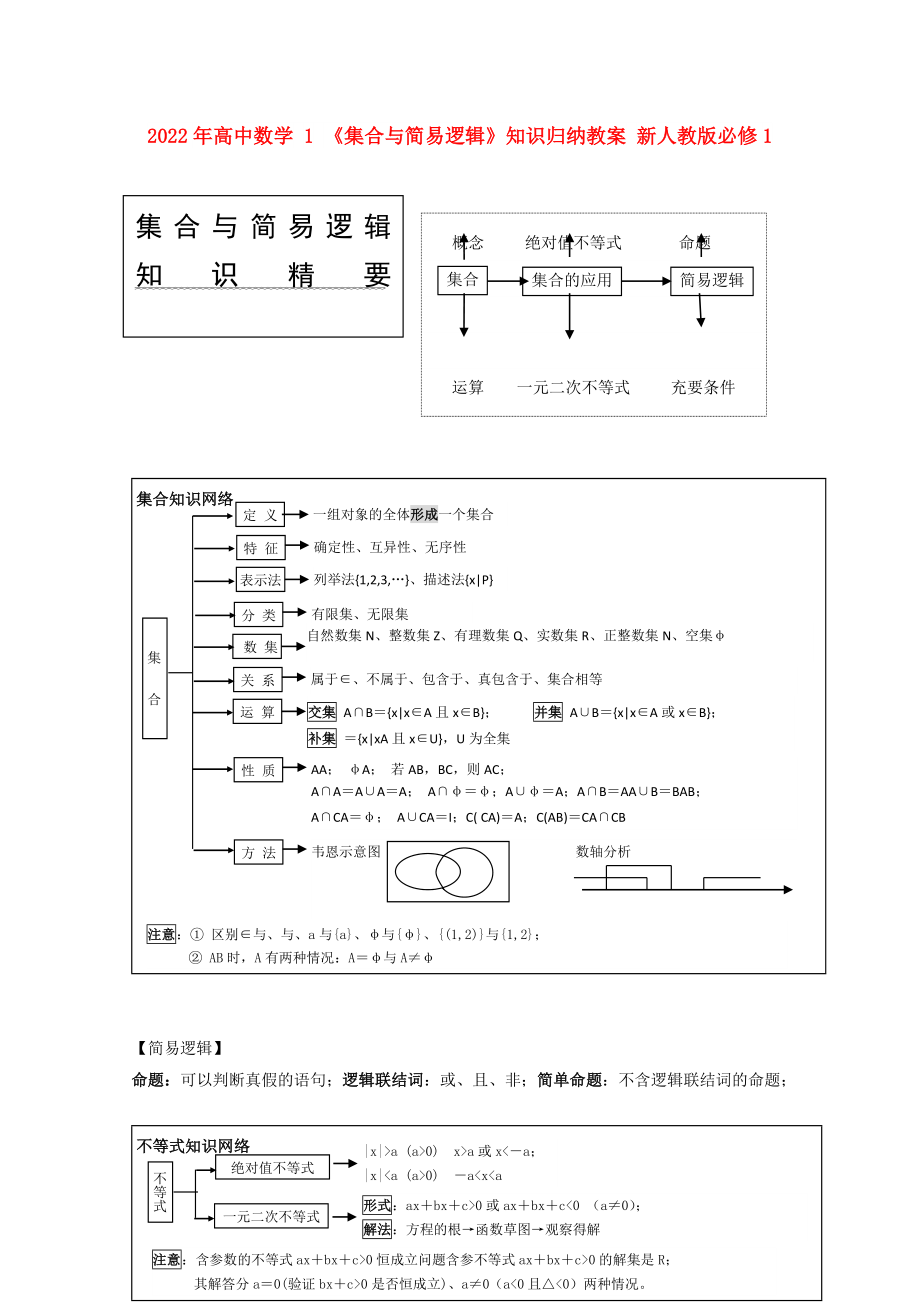
1、 2022年高中數(shù)學 1 《集合與簡易邏輯》知識歸納教案 新人教版必修1 集合與簡易邏輯 知識精要 概念 絕對值不等式 命題 集合的應用 簡易邏輯 集合 運算 一元二次不等式 充要條件 集 合 定 義 特 征 一組對象的全體形成一個集合 確定性、互異性、無序性 表示法 分 類 列舉法{1,2,3,…}、描述法{x|P} 有限集、無限集 數(shù) 集 關 系 自然數(shù)集N、整數(shù)集Z、有理數(shù)集Q、實數(shù)集R、正整數(shù)集N、空集φ 屬于∈、不屬于、包含于、真包含于、集合相等 運

2、 算 性 質(zhì) 交集 A∩B＝{x|x∈A且x∈B}； 并集 A∪B＝{x|x∈A或x∈B}； 補集 ＝{x|xA且x∈U}，U為全集 AA； φA； 若AB，BC，則AC； A∩A＝A∪A＝A； A∩φ＝φ；A∪φ＝A；A∩B＝AA∪B＝BAB； A∩CA＝φ； A∪CA＝I；C( CA)＝A；C(AB)＝CA∩CB 方 法 韋恩示意圖 數(shù)軸分析 注意：① 區(qū)別∈與、與、a與{a}、φ與{φ}、{(1,2)}與{1,2}； ② AB時，A有兩種情況：A＝φ與A≠φ 集合知識網(wǎng)絡 不等式 絕

3、對值不等式 一元二次不等式 |x|>a (a>0) x>a或x<－a； |x|0) －a0或ax＋bx＋c<0 （a≠0）； 解法：方程的根→函數(shù)草圖→觀察得解 注意：含參數(shù)的不等式ax＋bx＋c>0恒成立問題含參不等式ax＋bx＋c>0的解集是R； 其解答分a＝0(驗證bx＋c>0是否恒成立)、a≠0（a<0且△<0）兩種情況。 不等式知識網(wǎng)絡 【簡易邏輯】 命題：可以判斷真假的語句； 邏輯聯(lián)結(jié)詞：或、且、非； 簡單命題：不含邏輯聯(lián)結(jié)詞的命題； 復合命題：由簡單命題與邏輯聯(lián)結(jié)詞構成的命題。 三種形式：p或q、p且q、非p 真假判斷：p或q，同假為假，否則為真；p且q，同真為真；非p，真假相反 原命題：若p則q； 逆命題：若q則p； 否命題：若p則q； 逆否命題：若q則p； 互為逆否的兩個命題是等價的。 反證法步驟：假設結(jié)論不成立→推出矛盾→假設不成立。

展開閱讀全文
溫馨提示:
1: 本站所有資源如無特殊說明，都需要本地電腦安裝OFFICE2007和PDF閱讀器。圖紙軟件為CAD,CAXA,PROE,UG,SolidWorks等.壓縮文件請下載最新的WinRAR軟件解壓。
2: 本站的文檔不包含任何第三方提供的附件圖紙等，如果需要附件，請聯(lián)系上傳者。文件的所有權益歸上傳用戶所有。
3.本站RAR壓縮包中若帶圖紙，網(wǎng)頁內(nèi)容里面會有圖紙預覽，若沒有圖紙預覽就沒有圖紙。
4. 未經(jīng)權益所有人同意不得將文件中的內(nèi)容挪作商業(yè)或盈利用途。
5. 裝配圖網(wǎng)僅提供信息存儲空間，僅對用戶上傳內(nèi)容的表現(xiàn)方式做保護處理，對用戶上傳分享的文檔內(nèi)容本身不做任何修改或編輯，并不能對任何下載內(nèi)容負責。
6. 下載文件中如有侵權或不適當內(nèi)容，請與我們聯(lián)系，我們立即糾正。
7. 本站不保證下載資源的準確性、安全性和完整性, 同時也不承擔用戶因使用這些下載資源對自己和他人造成任何形式的傷害或損失。

相關資源

更多
正為您匹配相似的精品文檔
關于我們 - 網(wǎng)站聲明 - 網(wǎng)站地圖 - 資源地圖 - 友情鏈接 - 網(wǎng)站客服 - 聯(lián)系我們

copyright@ 2023-2025  zhuangpeitu.com 裝配圖網(wǎng)版權所有   聯(lián)系電話：18123376007

備案號:蜀ICP備2024067431號-1 川公網(wǎng)安備51140202000466號


本站為文檔C2C交易模式，即用戶上傳的文檔直接被用戶下載，本站只是中間服務平臺，本站所有文檔下載所得的收益歸上傳人(含作者)所有。裝配圖網(wǎng)僅提供信息存儲空間，僅對用戶上傳內(nèi)容的表現(xiàn)方式做保護處理，對上載內(nèi)容本身不做任何修改或編輯。若文檔所含內(nèi)容侵犯了您的版權或隱私，請立即通知裝配圖網(wǎng)，我們立即給予刪除！